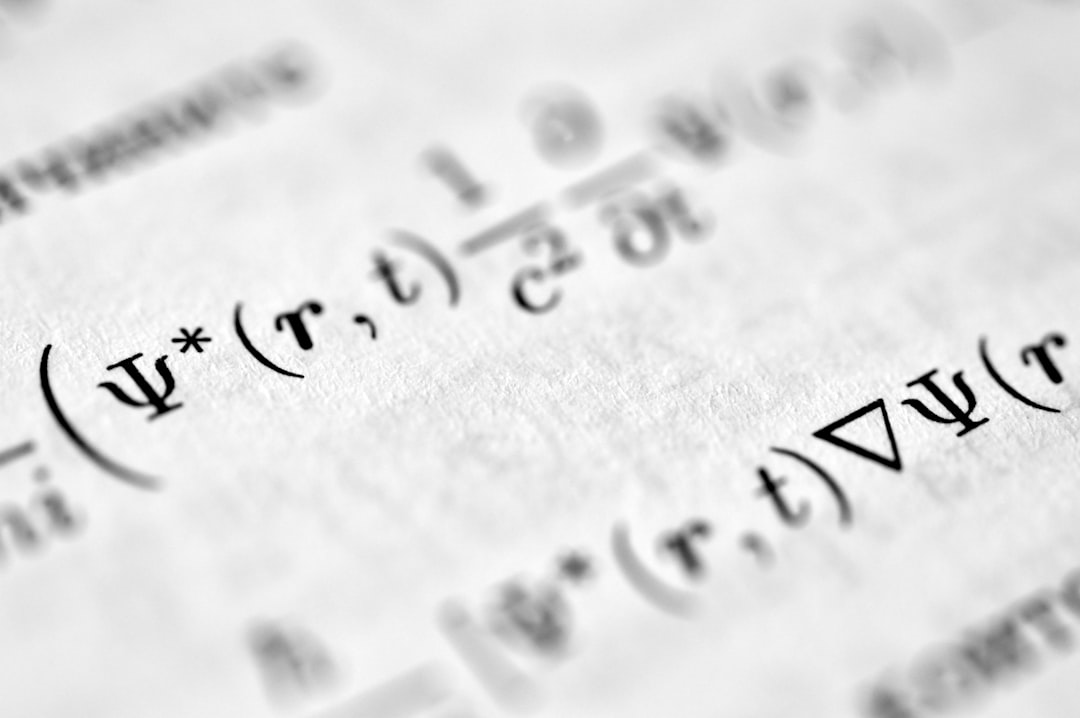The Quantum No-Signaling Principle (QNS) stands as a foundational tenet in quantum mechanics and quantum information theory, dictating a fundamental limitation on the speed and nature of information transfer. It asserts that local measurements performed on entangled quantum systems cannot be used to transmit information faster than the speed of light, even when those systems exhibit correlations that transcend classical physics. This principle is not merely an empirical observation but a logical consequence of the mathematical framework of quantum mechanics, preventing the scenario of “spooky action at a distance” from being exploited for superluminal communication. Its implications are profound, shaping our understanding of causality, locality, and the very fabric of reality at its most fundamental level.
Superluminal Communication and its Paradoxes
The concept of superluminal communication, or transmitting information faster than the speed of light, presents significant challenges to the established principles of causality and special relativity. If one could send a message instantaneously, it would become possible to send information into one’s own past, leading to a host of logical paradoxes. Imagine receiving a message informing you of a stock market crash before it happens, allowing you to profit handsomely from foreknowledge. Such scenarios, often explored in science fiction, are robustly forbidden by the laws of physics as we understand them. The QNS principle directly addresses this potential loophole arising from quantum entanglement. You can learn more about the block universe theory in this insightful video.
Entanglement and its Peculiarities
Quantum entanglement describes a phenomenon where two or more quantum particles become interconnected in such a way that they share the same fate, regardless of the distance separating them. Measuring a property of one entangled particle instantaneously influences the state of the other, even if they are light-years apart. This “spooky action at a distance,” as Albert Einstein famously called it, initially suggested the possibility of superluminal communication. However, the QNS principle clarifies that while the state of the distant particle changes instantaneously, this change cannot be controlled or manipulated to encode transmittable information.
The Role of Measurement Outcomes
The core of the QNS principle lies in the probabilistic nature of quantum measurement outcomes. When a measurement is performed on an entangled particle, the outcome is inherently random, even though the state of the distant particle also changes instantaneously. An observer at location A, measuring their particle, cannot choose the outcome of their measurement. They are merely observing a random result from a predetermined set of possibilities. This randomness is crucial; without it, one could potentially encode information by manipulating the probabilities of distant outcomes.
The no signaling principle in quantum mechanics asserts that information cannot be transmitted faster than the speed of light, even when entangled particles are involved. This principle has significant implications for quantum communication and cryptography. For a deeper understanding of this concept and its applications, you can explore the related article available at this link.
Mathematical Formulation of No-Signaling
Joint Probabilities and Local Operations
Mathematically, the QNS principle is expressed through the constraints it imposes on joint probability distributions of measurement outcomes. Consider two spatially separated parties, Alice and Bob, who share an entangled state. Alice performs a measurement with setting $x$ and obtains outcome $a$. Bob performs a measurement with setting $y$ and obtains outcome $b$. The joint probability of these outcomes is denoted as $P(a, b | x, y)$.
Alice’s Perspective: Independence from Bob’s Choices
From Alice’s perspective, without any information about Bob’s measurements, the probability of her obtaining outcome $a$ for a given setting $x$ must be independent of Bob’s measurement setting $y$. This can be written as:
$P(a | x) = \sum_{b} P(a, b | x, y)$
The crucial point here is that this sum, representing Alice’s marginal probability, must be independent of $y$. In essence, Alice cannot infer anything about Bob’s chosen measurement setting by simply looking at her own measurement results. Her statistical distribution of outcomes remains the same, regardless of what Bob is doing.
Bob’s Perspective: Independence from Alice’s Choices
Symmetrically, from Bob’s perspective, the probability of his obtaining outcome $b$ for a given setting $y$ must be independent of Alice’s measurement setting $x$. This is expressed as:
$P(b | y) = \sum_{a} P(a, b | x, y)$
Again, this sum must be independent of $x$. Bob’s local statistics provide no clues about Alice’s actions. These two conditions collectively define the quantum no-signaling principle. They act as a firewall, preventing any information flow between Alice and Bob through their shared entangled state alone.
Distinguishing Quantum No-Signaling from Classical Signaling

Classical Correlations vs. Entanglement
In the classical world, correlations between events can arise from shared past causes, but these correlations do not imply instantaneous influence. For example, if two individuals leave a house at the same time, one turning left and the other right, their paths are correlated. However, if one decides to run, it doesn’t instantly cause the other to run. Such correlations do not allow for superluminal communication. Entanglement, however, exhibits correlations that are stronger than anything achievable classically, yet without violating no-signaling.
The Bell Inequalities and Non-locality
The strength of quantum correlations is famously revealed by the violation of Bell inequalities. These inequalities provide a mathematical boundary for the correlations that can be explained by local hidden variable theories, which are classical in nature. Quantum entangled states routinely violate these inequalities, demonstrating a form of non-local correlation that cannot be explained by classical means. Despite this non-locality, the QNS principle ensures that this “spooky action” cannot be harnessed for faster-than-light communication.
Information Transfer Mechanisms
To send classical information, one typically needs a physical medium – an electromagnetic wave, a sound wave, or a tangible object – that propagates through space. The speed of this propagation is bounded by the speed of light. In quantum mechanics, while the state collapse is instantaneous, the information about that collapse cannot be extracted locally. To know what Alice measured, Bob needs to receive a classical message from Alice, informing him of her measurement setting and outcome. This classical message is bound by the speed of light, effectively preserving causality.
Implications and Consequences

Preservation of Causality
The most direct and significant implication of the QNS principle is the preservation of causality. Without this principle, the very concept of cause and effect would be undermined. If information could travel backward in time, or faster than light, the universe would become a chaotic and unpredictable place, devoid of any consistent temporal order. The QNS principle acts as a cosmic speed limit for information, ensuring that events unfold in a consistent and predictable sequence, even in the presence of quantum weirdness.
Limits on Quantum Information Processing
While entanglement is a powerful resource for quantum computation and communication, the QNS principle imposes fundamental limits on what can be achieved. It means that entanglement itself cannot be used to establish a superluminal communication channel. This has important consequences for the design of quantum communication networks and quantum cryptographic protocols, where the security often relies on the no-signaling property. Quantum key distribution, for instance, leverages the non-signaling property to guarantee the security of shared cryptographic keys. An eavesdropper attempting to intercept the quantum key cannot gain information without disturbing the entangled state, and this disturbance is detectable due to the no-signaling property.
Constraints on Alternative Theories
The QNS principle also acts as a powerful constraint on the development of alternative theories of quantum mechanics. Any proposed theoretical framework that aims to supersede or extend quantum mechanics must either explicitly or implicitly incorporate the no-signaling condition. Theories that attempt to reintroduce local hidden variables, for instance, often struggle to reproduce quantum correlations without violating no-signaling. This principle thus serves as a critical litmus test for the consistency and validity of new physical theories.
The no signaling principle in quantum mechanics is a fascinating topic that explores the limitations of information transfer between entangled particles. This principle asserts that measurements performed on one particle cannot instantaneously affect the state of another, regardless of the distance separating them. For a deeper understanding of this concept and its implications in the realm of quantum communication, you can read a related article on the subject at My Cosmic Ventures. This resource provides valuable insights into how the no signaling principle shapes our understanding of quantum entanglement and its applications.
No-Signaling and Other Fundamental Principles
| Metric | Description | Value / Range | Unit | Relevance to No Signaling Principle |
|---|---|---|---|---|
| Speed of Information Transfer | Maximum speed at which information can be transmitted | ≤ 299,792,458 | km/s (speed of light) | Ensures no faster-than-light signaling, consistent with no signaling principle |
| Bell Inequality Violation | Degree to which quantum correlations exceed classical limits | Up to 2√2 (~2.828) | CHSH parameter | Shows quantum entanglement but does not allow signaling |
| Quantum State Collapse | Instantaneous change in state upon measurement | Instantaneous (theoretical) | Time | Nonlocal but does not transmit usable information, preserving no signaling |
| Communication Capacity | Amount of classical information transmitted via entanglement alone | 0 | bits | Entanglement cannot be used for signaling without classical communication |
| Measurement Outcome Correlation | Correlation coefficient between entangled particles’ measurements | Up to ±1 | Correlation coefficient | Strong correlations exist but do not enable signaling |
Connection to Locality and Reality
The QNS principle is intricately linked to the concepts of locality and reality, which have been central to philosophical debates in quantum mechanics. While quantum mechanics demonstrably exhibits non-local correlations, the no-signaling principle ensures that this non-locality does not lead to a violation of relativistic locality in terms of information transfer. It implies that while entangled particles are non-locally connected, they cannot be used to violate the local causality required by special relativity. This delicate balance allows for the peculiar nature of quantum reality without creating paradoxical scenarios.
Quantum Field Theory and its Consistency
In the realm of quantum field theory (QFT), the no-signaling principle is a fundamental requirement for the consistency of the theory. QFT, which combines quantum mechanics with special relativity, naturally incorporates the speed of light limit. Violations of no-signaling within QFT would imply fundamental inconsistencies in the commutation relations of field operators or other core aspects of the theory. The consistency of QFT, a highly successful framework for describing fundamental particles and forces, thus indirectly reinforces the validity of the quantum no-signaling principle.
Operational Interpretations
From an operational perspective, the no-signaling principle is a statement about what can and cannot be achieved by experimentalists. It suggests that despite the seemingly instantaneous correlations between entangled particles, an experimenter at one location cannot influence the statistical outcomes observed by an experimenter at another remote location through their local measurements alone. This operational constraint is crucial for the very possibility of conducting localized experiments and for the overall consistency of scientific inquiry.
In conclusion, the Quantum No-Signaling Principle is more than just a mathematical curiosity; it is a cornerstone of modern physics, upholding the very fabric of causality and supporting the consistency of quantum mechanics with special relativity. It acts as a gatekeeper, preventing the exploitation of quantum entanglement for superluminal communication and ensuring that the universe operates under a consistent set of rules. As we continue to explore the mysteries of the quantum realm, the no-signaling principle will remain a guiding light, illuminating the boundaries of what is physically possible and shaping our understanding of reality itself.
FAQs
What is the no signaling principle in quantum mechanics?
The no signaling principle states that information cannot be transmitted faster than the speed of light, ensuring that quantum entanglement cannot be used for instantaneous communication between distant parties.
How does the no signaling principle relate to quantum entanglement?
While quantum entanglement creates strong correlations between particles, the no signaling principle ensures that these correlations cannot be exploited to send messages instantaneously, preserving causality in quantum theory.
Why is the no signaling principle important in quantum physics?
It maintains consistency with the theory of relativity by preventing faster-than-light communication, thereby upholding the causal structure of spacetime and ensuring that quantum mechanics does not violate fundamental physical laws.
Can the no signaling principle be violated in any quantum experiments?
No, all experimental results to date confirm that the no signaling principle holds true, and no quantum experiment has demonstrated the ability to transmit information faster than light.
Does the no signaling principle limit quantum computing or quantum communication?
No, it does not limit the capabilities of quantum computing or quantum communication; rather, it sets fundamental constraints on how information can be transmitted, ensuring that quantum technologies operate within the bounds of relativistic causality.
Is the no signaling principle unique to quantum mechanics?
While the principle is crucial in quantum mechanics, it is a general physical principle consistent with special relativity and applies to all physical theories that respect causality and the speed of light limit.
How is the no signaling principle mathematically expressed?
Mathematically, it is expressed by the condition that the marginal probability distribution of measurement outcomes on one subsystem does not depend on the choice of measurement performed on a distant subsystem.
What role does the no signaling principle play in quantum cryptography?
It ensures the security of quantum cryptographic protocols by preventing eavesdroppers from exploiting entanglement to gain information instantaneously, thereby preserving the integrity of secure communication.