Error correction codes (ECC) are fundamental tools in information theory and telecommunications that detect and correct errors occurring during data transmission or storage. These codes protect against noise and interference that can corrupt data, preserving information integrity. Error correction is a critical component of modern communication systems, enabling reliable data exchange across digital communications, computer memory systems, and other platforms.
Error correction codes significantly impact system performance beyond data integrity alone. They enhance the efficiency and reliability of systems that depend on accurate information processing. As technology advances and data volume increases, robust error correction mechanisms become increasingly important.
Consequently, understanding error correction code principles and applications is essential for researchers and professionals in computer science, physics, and related fields.
Key Takeaways
- Error correction codes are essential for detecting and correcting errors in data transmission and storage, crucial in both classical and quantum physics.
- Classical error correction codes include methods like parity checks and Reed-Solomon codes, while quantum error correction codes address unique quantum errors.
- Error correction is vital in quantum computing to maintain qubit integrity and enable reliable quantum information processing.
- Applications span experimental physics, improving measurement accuracy and data reliability in complex experiments.
- Ongoing research focuses on overcoming current limitations, enhancing code efficiency, and developing new codes for future quantum technologies.
The Importance of Error Correction in Physics
In the field of physics, particularly in experimental and theoretical research, the accuracy of data is paramount.
These inaccuracies can lead to flawed conclusions and hinder scientific progress.
Therefore, implementing effective error correction strategies is crucial for ensuring that experimental results are reliable and reproducible. Moreover, as physicists delve into increasingly complex systems, such as quantum mechanics and high-energy particle physics, the need for sophisticated error correction becomes even more pronounced. In these domains, the stakes are high; a single erroneous measurement can derail years of research.
Consequently, error correction codes not only enhance the quality of data but also foster confidence in scientific findings, allowing researchers to build upon each other’s work with assurance.
Types of Error Correction Codes
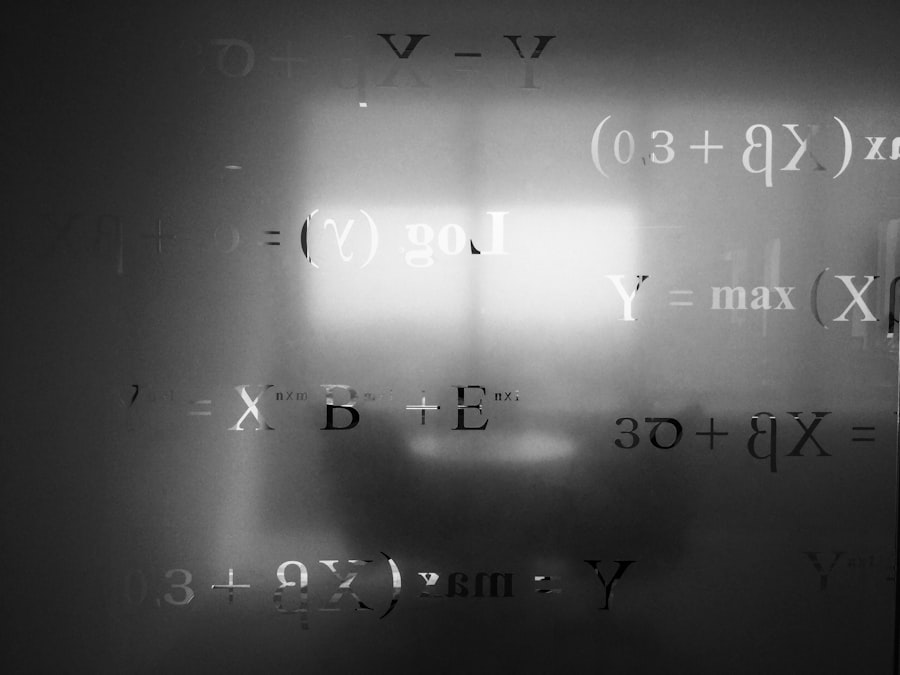
Error correction codes can be broadly categorized into two main types: block codes and convolutional codes. Block codes operate on fixed-size blocks of data, adding redundancy to each block to facilitate error detection and correction. This method allows for straightforward implementation and is widely used in various applications, including data storage and transmission protocols.
The simplicity of block codes makes them an attractive choice for many systems, as they can be easily integrated into existing frameworks. On the other hand, convolutional codes process data streams continuously rather than in discrete blocks. They utilize a sliding window approach to encode information, which allows for greater flexibility in handling varying data rates.
Convolutional codes are particularly effective in scenarios where real-time error correction is necessary, such as in satellite communications or mobile networks.
Classical Error Correction Codes
Classical error correction codes have been foundational in the development of reliable communication systems. Among the most well-known classical codes are Hamming codes, Reed-Solomon codes, and Turbo codes. Hamming codes are particularly notable for their ability to detect and correct single-bit errors within a block of data.
They achieve this by adding parity bits that provide redundancy, allowing the receiver to identify and correct errors without needing to retransmit the entire message. Reed-Solomon codes, on the other hand, are widely used in applications such as CDs, DVDs, and QR codes due to their robustness against burst errors. These codes operate on symbols rather than individual bits, making them highly effective for correcting errors that occur in clusters.
Turbo codes represent a more recent advancement in classical error correction techniques, employing iterative decoding processes to achieve near-optimal performance. Their ability to approach the Shannon limit—the theoretical maximum efficiency of data transmission—has made them a popular choice in modern communication systems.
Quantum Error Correction Codes
| Code Type | Physical Implementation | Error Model | Code Rate | Typical Use Case | Key Metric |
|---|---|---|---|---|---|
| Shor Code | Trapped Ions / Superconducting Qubits | Bit-flip and Phase-flip errors | 1/9 | Quantum memory stabilization | Corrects 1 qubit error |
| Surface Code | Superconducting Qubits on 2D Lattice | Local Pauli errors | ~0.5 | Fault-tolerant quantum computing | Error threshold ~1% |
| Reed-Muller Code | Optical Quantum Systems | Depolarizing noise | Variable | Quantum communication | Distance and rate trade-off |
| CSS Code | Superconducting and Ion Trap Qubits | Bit-flip and Phase-flip errors | Variable | Quantum error correction in algorithms | Logical error rate reduction |
| Hamming Code (Classical) | Classical Electronics | Single-bit errors | k/(k+log2(k+1)) | Classical error correction | Corrects 1 bit error |
As quantum computing emerges as a transformative technology, the need for quantum error correction codes has become increasingly critical. Quantum systems are inherently susceptible to errors due to decoherence and other quantum noise phenomena. Unlike classical bits, which can be simply flipped from 0 to 1 or vice versa, quantum bits (qubits) exist in superpositions of states, making error correction more complex.
Quantum error correction codes address these challenges by encoding logical qubits into entangled states of multiple physical qubits. One prominent example is the Shor code, which can correct arbitrary single-qubit errors by using redundancy across multiple qubits. This innovative approach not only protects quantum information but also enables fault-tolerant quantum computation—a crucial requirement for realizing practical quantum computers.
As researchers continue to explore new quantum error correction techniques, they pave the way for advancements in quantum technologies that could revolutionize computing and information processing.
Applications of Error Correction Codes in Physics
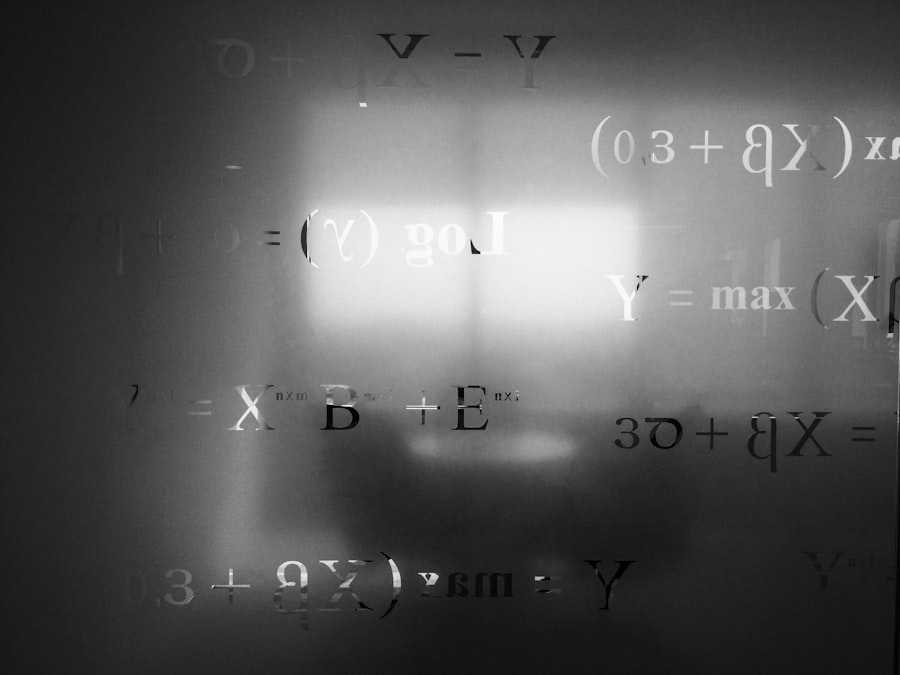
Error correction codes find diverse applications across various branches of physics. In experimental physics, they are employed to ensure the accuracy of measurements obtained from sensitive instruments. For instance, in high-energy particle physics experiments conducted at facilities like CERN, error correction techniques are vital for analyzing vast amounts of data generated during particle collisions.
By applying these codes, physicists can filter out noise and focus on meaningful signals that contribute to groundbreaking discoveries. In astrophysics, error correction codes play a crucial role in processing data collected from telescopes and satellites. The vast distances involved in astronomical observations introduce significant challenges related to signal degradation and interference.
By utilizing advanced error correction techniques, researchers can enhance the quality of astronomical data, leading to more accurate models of celestial phenomena and a deeper understanding of the universe.
Challenges and Limitations of Error Correction Codes
Despite their numerous advantages, error correction codes are not without challenges and limitations. One significant issue is the trade-off between redundancy and efficiency. While adding redundancy improves error detection and correction capabilities, it also increases the amount of data that must be transmitted or stored.
This can lead to inefficiencies in bandwidth usage or storage capacity, particularly in systems where resources are limited. Additionally, the complexity of implementing certain error correction codes can pose challenges for practical applications. For instance, while quantum error correction codes offer robust protection against errors in quantum systems, they require intricate encoding and decoding processes that can be computationally intensive.
As researchers strive to develop more efficient algorithms for error correction, they must balance performance with practicality to ensure that these techniques can be effectively integrated into real-world systems.
Recent Advances in Error Correction Codes
Recent advancements in error correction codes have been driven by the increasing demand for reliable communication systems in an era characterized by rapid technological growth. Researchers have made significant strides in developing new coding techniques that enhance performance while minimizing resource consumption. For example, low-density parity-check (LDPC) codes have gained popularity due to their ability to achieve near-capacity performance with relatively simple decoding algorithms.
Moreover, machine learning techniques are being explored as potential tools for improving error correction processes. By leveraging artificial intelligence algorithms, researchers aim to optimize coding strategies dynamically based on real-time data conditions. This innovative approach could lead to more adaptive error correction methods that respond effectively to varying levels of noise and interference.
Error Correction Codes in Quantum Computing
In the realm of quantum computing, error correction codes are indispensable for maintaining the integrity of quantum information over extended periods. As qubits are prone to errors due to environmental interactions and operational imperfections, implementing robust error correction strategies is essential for achieving fault-tolerant quantum computation. Techniques such as surface codes have emerged as promising solutions due to their scalability and efficiency in correcting multiple qubit errors simultaneously.
Furthermore, ongoing research into topological quantum computing has opened new avenues for developing error-resistant qubits that inherently protect against certain types of errors. By harnessing the principles of topology, these qubits could potentially simplify the implementation of error correction codes while enhancing overall system reliability.
Error Correction Codes in Experimental Physics
In experimental physics, where precision is paramount, error correction codes serve as critical tools for ensuring accurate data collection and analysis. For instance, in experiments involving atomic clocks or gravitational wave detectors, even minor errors can lead to significant discrepancies in results. By employing sophisticated error correction techniques, physicists can mitigate these risks and enhance the reliability of their findings.
Additionally, as experimental setups become increasingly complex—incorporating multiple sensors and data streams—error correction codes help streamline data processing workflows. By filtering out noise and correcting errors in real-time, researchers can focus on extracting meaningful insights from their experiments without being bogged down by unreliable data.
Future Perspectives and Developments in Error Correction Codes
Looking ahead, the future of error correction codes appears promising as researchers continue to explore innovative approaches to enhance their effectiveness across various domains. The integration of artificial intelligence into coding strategies holds great potential for developing adaptive systems capable of responding dynamically to changing conditions. Moreover, as quantum technologies advance further into mainstream applications, the demand for efficient quantum error correction methods will only grow.
Researchers will likely focus on refining existing techniques while exploring novel coding paradigms that leverage emerging technologies such as topological qubits or hybrid quantum-classical systems. In conclusion, error correction codes represent a vital component of modern communication systems and experimental physics alike. Their ability to detect and correct errors ensures the integrity of information across diverse applications—from classical telecommunications to cutting-edge quantum computing technologies.
As advancements continue to unfold in this field, researchers remain committed to overcoming challenges and unlocking new possibilities for reliable information processing in an increasingly complex world.
Error correction codes play a crucial role in various fields of physics, particularly in quantum computing and information theory. For a deeper understanding of how these codes can enhance data integrity and reliability in quantum systems, you can explore the article on this topic at this link. This resource provides valuable insights into the principles and applications of error correction codes in modern physics.
FAQs
What are error correction codes in physics?
Error correction codes in physics refer to mathematical techniques used to detect and correct errors in data transmission or storage, ensuring the integrity of information despite noise or disturbances.
Why are error correction codes important in physics?
They are crucial for maintaining accurate data in experiments, quantum computing, and communication systems, where physical processes can introduce errors that compromise results or operations.
How do error correction codes work?
These codes add redundant information to the original data, allowing the detection and correction of errors by comparing received data against expected patterns or parity checks.
What types of error correction codes are commonly used in physics?
Common types include Hamming codes, Reed-Solomon codes, and quantum error correction codes like the Shor code and surface codes, each suited for different applications and error models.
What is the difference between classical and quantum error correction codes?
Classical codes correct errors in classical bits, while quantum error correction codes protect quantum bits (qubits) from decoherence and other quantum noise, preserving quantum information.
Can error correction codes completely eliminate errors?
While they significantly reduce errors, no code can guarantee perfect correction in all cases; the effectiveness depends on the code design and the error rate of the system.
Where are error correction codes applied in physics?
They are applied in quantum computing, data transmission in particle physics experiments, satellite communications, and any system where data integrity is critical under physical noise.
What challenges exist in implementing error correction codes in physics?
Challenges include the complexity of code design, resource overhead, especially in quantum systems, and the need to balance error correction capability with system efficiency.
How do quantum error correction codes differ in complexity from classical ones?
Quantum codes must handle unique quantum errors like superposition and entanglement disturbances, making them more complex and resource-intensive than classical codes.
Are error correction codes only theoretical, or are they used in practical physics applications?
They are widely used in practical applications, including quantum computers under development, communication satellites, and experimental physics setups requiring high data fidelity.
